
数学中有许多令人着迷的难题,有些难题本身晦涩深奥,连问题的陈述都需要扎实的专业背景才能读懂。比如,解析数论中的黎曼猜想,代数几何的霍奇猜想,数论与代数几何交织的abc 猜想,或者关于流体力学的纳维–斯托克斯方程平滑性与存在性问题。这些问题的陈述往往夹杂着高等数学的语言,让人一眼望去就觉其深不可测。
但也有一些难题,陈述简单到让人惊讶,几乎人人都能理解它们的规则。比如,关于素数分布的孪生素数猜想,声名远扬的哥德巴赫猜想等等。这些难题不需要任何高深的数学工具,只要会最基础的加减乘除,就能立刻明白题目的意思。

另一个令人难以置信的简单的棘手问题,就是科拉茨猜想。它的表述极其简单,但却异常困难。沃尔夫冈·保利曾经谈到科拉茨猜想时说过,数学或许还没有准备好去处理这样的问题。还有人认为,这是一道极其困难、完全超出当代数学能力范围的难题——这是2010年的评价。然而,尽管如此,数学家们已经在它的边缘取得了一些进展。
要解释科拉茨猜想,先从一个简单的过程说起。选取任意一个自然数,比如 13,然后按照以下步骤进行运算:
如果这个数是偶数,就除以 2;
如果这个数是奇数,就乘以 3 再加 1。
偶数因此变小,奇数则会增大。以 13 为例,13 乘以 3 是 39,再加 1 得到 40。40 是偶数,除以 2 得到 20;20 仍是偶数,继续除以 2 得到 10;10 除以 2 得到 5;5 是奇数,乘以 3 再加 1 得到 16;接着 16 变成 8,8 变成 4,4 变成 2,2 变成 1。从 1 开始,这个过程就会陷入循环:1,4,2,1,4,2,1……无休无止。
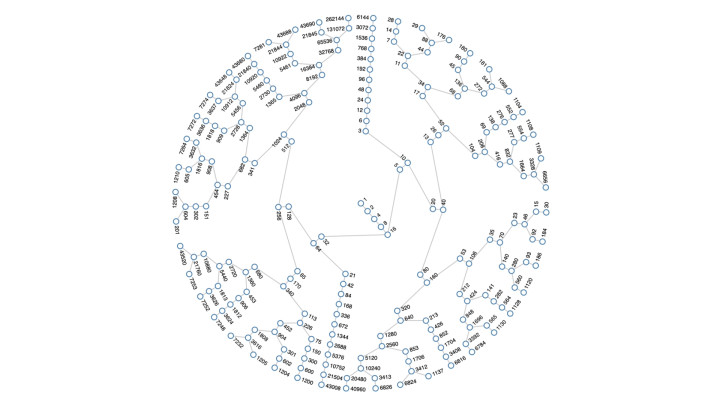
这样的数列常常被称为 冰雹序列(hailstone sequences)。原因在于,这个过程类似于一种过于简化的冰雹形成模型:一小块冰晶最初在云中生成,然后被气流推动上下翻飞。有时温度足够低时,它会积累更多冰晶;有时又会稍稍融化。这样的上下运动,最终造就了一颗部分融化的冰雹,直到它足够重,坠向地面。科拉茨猜想正是类比了这一过程:无论起始的数字多么庞大,哪怕是百万甚至亿级的数,经过这样的上下波动,最终都会落地,归于那个无限循环的 1-4-2 序列。
如果把这些序列绘制成图,你会看到它们的走势就像 布朗运动(Brownian motion),又像金融市场的曲线,毫无规律地上升与下跌。事实上,这个现象是可以解释的:如果随机选择一个数字开始迭代,序列的行为在最初阶段非常类似于 随机游走(random walk),只不过带有轻微的 下行趋势(downward drift)。这就像在赌场里反复下注轮盘赌,当赔率略微对你不利时,你可能偶尔赢一局,但从长远来看,你输的次数一定比赢的多,钱包的余额总会逐渐缩减。
统计学从这个角度支持了科拉茨猜想的合理性。数学家们利用概率论证明,大约 99% 的数字 最终都会下降,虽然不一定精准地降到 1,但肯定会比起始值小得多。这就好像告诉你:在赌场里玩得足够久,绝大多数情况下,你的钱都会比开始时更少。这就是目前得到的数学结果。
然而,为什么这条概率论的思路无法直接推进,完全证明猜想呢?症结在于,概率论的推理总是会留下 例外事件(exceptional events) 的余地。概率论中的 大数定律(law of large numbers) 告诉我们,如果长期参与一个赔率不利的博弈,几乎可以确定最终会输光钱。然而“几乎”并不是“绝对”。理论上,总有极少数情况,赌徒可能不断略微多赢于输,突破常规。
这正是科拉茨猜想难以攻克的原因所在。就像 纳维–斯托克斯(Navier–Stokes)方程 中的现象一样,大多数初始条件下,解会平稳演化并消散,但某些极端特殊的条件可能导致“爆炸”。同样,或许真的存在某个极其特殊的数字,输入这个简单算法后,会像一架比空气还重的飞行器,持续上升,永不坠落。
更有趣的是,从二进制角度观察这些迭代,人们发现它们的演化规律和 元胞自动机(cellular automata) 非常相似,甚至像极了著名的 生命游戏(Game of Life)。生命游戏能够演化出复杂的、自我复制的巨大结构,科拉茨过程似乎也蕴含着类似的潜力。数学家 约翰·康威(John Conway) 曾深入研究过这个问题。他考虑了科拉茨问题的推广形式——不再只是“奇数乘3加1、偶数除以2”,而是设定更多分支,比如 17 种不同的操作。康威证明,只要迭代规则足够复杂,就可以在这个过程中 编码图灵机(Turing machines),使得这个问题变得 不可判定(undecidable)。
康威甚至为这些分式线性变换发明了一种编程语言,命名为 Factran,取 fraction 和 Fortran 的谐音。他用这个语言构造过程序:如果输入的数字编码成素数,序列会一路下行到底;如果不是,则会不断上升。换句话说,这类问题的总体复杂性,几乎等同于整个数学的复杂性。
由此可见,科拉茨猜想并非一条孤立的数学难题,而是与复杂性理论、动力系统乃至可计算性理论紧密交织在一起。或许,想要真正解决这个谜题,需要一套全新的数学框架——不仅是统计学意义上的“几乎确定”,而是可以严密证明 所有数字 都会最终收敛的理论。
在当今数学界,科拉茨猜想与 黎曼假设(Riemann Hypothesis)、P vs NP 问题 并列,被视为最著名、也最深奥的开放问题之一。黎曼假设是数论皇冠上的明珠,而 P vs NP 问题则是一个“元问题”,因为如果 P=NP 成立,意味着我们有可能高效解决许多原本难以触及的复杂问题。科拉茨猜想,就像一道静静矗立的高墙,用极其朴素的语言揭示了数学深渊的无限魅力。
爱配资-股票杠杆10倍-配资入门炒股-配资靠谱证券配资门户提示:文章来自网络,不代表本站观点。